闽南师范大学2018年硕士研究生入学考试
《分析与代数》考试大纲
一、考试基本要求:
考察学生对《数学分析》和《高等代数》的基本理论、基本方法和基本技能的掌握程度;考察学生抽象思维、逻辑推理和分析、解决问题的能力。
二、考试方法和时间
考试方法为笔试,考试时间为3个小时。
三、考核知识点
(一)数列极限、函数极限的定义及性质;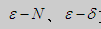 方法的证明;数列极限、函数极限的各种计算方法
方法的证明;数列极限、函数极限的各种计算方法
(二)连续性的定义及性质;连续性、一致连续性的证明及其应用
(三)微分和导数的概念及导数的几何意义;微分中值定理、Taylor公式、不等式的证明及导数在研究函数中的应用
(四)不定积和定积分的定义;积分中值定理、牛顿-莱布尼兹公式、定积分的计算、证明、应用及积分等式或不等式证明,广义积分的计算。
(五)数项级数收敛、发散和函数项级数一致收敛的判别法;幂级数的收敛半径、收敛域、级数和的求法及函数的Taylor展开
(六)平面点集;二元函数极限、连续的定义及计算;多元函数偏导数及全微分的定义、计算及有关的证明
(七)二重积分、三重积分的计算;两类曲线积分、两类曲面积分的计算;格林公式、高斯公式的应用
(八) 整除理论:包括整除性、带余除法、最大公因式、互素的概念与性质;因式分解理论:包括不可约多项式、因式分解定理、重因式、实系数与复系数多项的因式分解,有理系数多项式不可约的判定;根的理论:包括多项式函数、多项式的根、有理系数多项式的有理根求法
(九)行列式的定义、性质;行列式的按行(列)展开定理;行列式的计算方法;克莱姆法则
(十)线性方程组的解法——消元法;数域P上n维向量空间Pn及向量的线性相关性;线性方程组有解的判别定理;线性方程组解的结构及齐次线性方程组的解空间的讨论
(十一)矩阵的运算;初等变换与初等矩阵;可逆矩阵;分块矩阵;矩阵的秩;矩阵的等价(即相抵)、合同、相似;矩阵的可对角化问题
(十二)线性空间的概念;基、维数与坐标;基变换与坐标变换;子空间、子空间的交与和、维数公式、子空间的直和;线性空间的同构
(十三) 线性映射与线性变换的概念、运算;线性变换的矩阵表示;线性变换(矩阵)的特征多项式、特征值与特征向量;线性变换的值域与核;不变子空间
(十四)二次型及其标准型,正定二次型。欧几里得空间概念,正交基、正交变换、实对称阵的标准型。
四、参考书目
华东师范大学数学系编,数学分析(上、下册)(第四版),高等教育出版社,2010年。
北京大学数学系几何与代数教研究前代数小组编,王萼芳、石生明修订《高等代数》(第三版),高等教育出版社2003。
闽南师范大学数学与统计学院
2017年9月