一、考查目标
要求考生掌握有关数学教学设计的基本知识、基础理论和基本方法,并能运用相关理论和方法分析、解决数学教学设计中的问题。
二、考试形式与试卷结构
(一)试卷成绩及考试时间
本试卷满分为100分。考试时间为180分钟。
(二)答题方式
答题方式为闭卷、笔试。
(三)试卷内容结构
各部分内容所占分值为:
数学教学设计的含义、理论依据和技术:约20分
数学基本课型的教学设计:约30分
常见的数学教学模式:约20分
数学问题解决的教学设计:约20分
数学活动课的教学设计:约10分
(四)试卷题型结构
简答题:共20分
论述题:共30分
教材分析:20分
教学设计:共30分
三、考查范围
(一)数学教学设计的含义、理论依据和技术
(1)考查目标
了解:数学设计的理念、思路、理论依据,数学教学内容分析和学生分析的思路。
理解:数学教学三维目标设计的内容,能清楚区分三维目标的层次。
掌握:数学教学设计的本质及意义。
(2)考查内容
1.数学教学设计的含义、思路、理念
2.数学教学设计的理论依据
3.数学教学设计的目标分析、内容分析、学生分析及教案的编写
(二)数学基本课型的教学设计
(1)考查目标
了解:概念教学和原理教学的本质,概念教学设计和原理教学设计的理念、思路、理论依据。
理解:概念教学设计和原理教学设计的基本要求和基本模式。
掌握:数学习题教学的基本要求。
(2)考查内容
1.数学概念教学设计
2.数学原理教学设计
3.数学习题教学设计
(三)常见的数学教学模式
(1)考查目标
了解:数学教学模式的含义。
理解:选择数学教学模式的依据。
掌握:数学教学模式的主要特征;数学教学模式的构成;讲练结合与复习总结两种教学模式的差别;引导探究与指导自学的教学模式的差别。
(2)考查内容
1.数学教学模式的含义、特征与类型
2.讲练结合的教学模式
3.引导探究的教学模式
4.讨论交流的教学模式
5.指导自学的教学模式
6.复习总结的教学模式
(四)数学问题解决的教学设计
(1)考查目标
了解:问题解决与解题的区别与联系;数学问题解决的探索途径;数学问题解决活动的心理特征;数学问题解决教学活动的过程及其特点;影响数学问题解决的因素;数学问题解决教学中教师角色的特征。
理解:问题的多重含义及特征;数学问题情境的含义及特征。
掌握:设计好的数学问题及数学问题情境;合理安排数学问题解决教学活动;合理设计教师在数学问题解决教学活动中的职能和任务;综合设计数学问题解决教学。
(2)考查内容
1.问题的含义、特征与类型
2.数学问题解决的概念、过程及影响因素
3.数学问题解决的教学设计
4.数学问题解决教学案例分析
(五)数学活动课的教学设计
(1)考查要求
了解:数学活动课的含义、价值及类型。
理解:数学探究课;数学建模课;数学实践课。
掌握:数学探究、数学建模和数学活动课的3种课型的设计思想和方法。
(2)考查内容
1.数学活动课的含义、功能及类型
2.数学探究课及其教学设计
3.数学建模课及其教学设计
4.数学实践课及其教学设计
四、样题
一、简答题(本大题共2小题,每小题10分,共20分)请仔细思考,然后回答后面的问题。
1.数学教学设计的目的是什么?完成数学教学设计,教师需要考虑哪几个方面?
2.在高一(1)班的“指数函数”教学中,张老师设置了如下情境:
某细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个,……,如果分裂一次需要10min,那么1个细胞1h后分裂成多少个细胞?
假设细胞分裂的次数为x,相应的细胞个数为y,则
当x=6时,。即一个细胞1h后分裂成64个细胞。
在上述例子中,x只能取正整数。我们还知道对于式子,x取负整数和0也是有意义的。
那么x能取分数甚至无理数吗?
请问上述“细胞分裂”实例对于学生学习指数函数有何作用?
二、论述题(本大题共30分)下面是有关初中统计内容的问题设计。请仔细思考,然后回答后面的问题。
某工厂有5个股东,100个工人。工人的工资总额与工厂的股东总利润见表1。该工厂老板根据表中数据,作出了统计图(见图1),并声称股东和工人“有福共享、有难同当”。真是这样吗?
结合你对义务教育数学课程标准的理解,谈谈该案例对学生数学思考的作用。
三、教材分析(本大题共20分)下面呈现了某高中教科书关于数学归纳法的内容(片段)。请仔细分析,回答后面提出的问题。
案例:数学归纳法及其应用举例
在前面,我们是这样推导首项为,公差为d的等差数列的通项公式的:
……
由此得到,等差数列的通项公式是
像这种由一系列有限的特殊事例得出一般结论的推理方法,通常叫做归纳法。用归纳法可以帮助我们从具体事例中发现一般规律,但应该注意,仅根据一系列有限的特殊事例所得出的一般结论有时是不正确的。例如,一个数列的通项公式是
容易验证
如果由此作成结论——对于任何,都成立,那就是错误的。事实上,
那么,怎样判断由归纳法得到的某些与正整数有关的数学命题的真假呢?如果我们设想:先证明当n取第一个值(假如=1)时命题成立,然后假设当时命题成立,并证明当时,命题也成立,那么就证明这个命题成立。因为证明了这一点,就可以断定这个命题对于n取第一个值后面所有正整数也都成立。这种证明方法叫做数学归纳法。
……
“数学归纳法”教学的重难点有哪些?试简要阐述你的看法。
四、教学设计(本大题共两小题,每小题15分,共30分)
1.抽样是统计分析的基础,进行统计分析时需要收集数据,但收集数据有时很困难,有时还有破坏性。因此,在“抽样方法”教学中,教师应以较多的实例让学生感受抽样统计的重要性和必要性。
请你根据上述教学要求,创设两个不同的有关抽样统计的必要性的问题情境。
2.下面是一个有关三角形分割的问题:
以三角形的顶点和它内部n个点为顶点作三角形,则原三角形被分割成2n+1个小三角形。
为了让学生通过探究解决上述问题,教师A设计了如下两个问题情境:
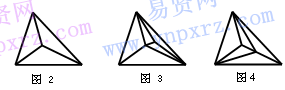
问题情境1:如图2,以三角形的顶点和它内部1个点为顶点作三角形,原三角形可以分割成几个小三角形?
问题情境2:如果在三角形中再添加一点,情况又怎样呢(见图3,图4)?照此下去,该三角形的分割情况又如何呢?从中你可以发现哪些数学问题?
请你预测一下当学生面对上述两个问题情境时,他们将作出何种数学反应。