初中数学知识点总结:二次函数的应用
2016-10-24来源:易贤网
知识点总结
一.二次函数的最值:
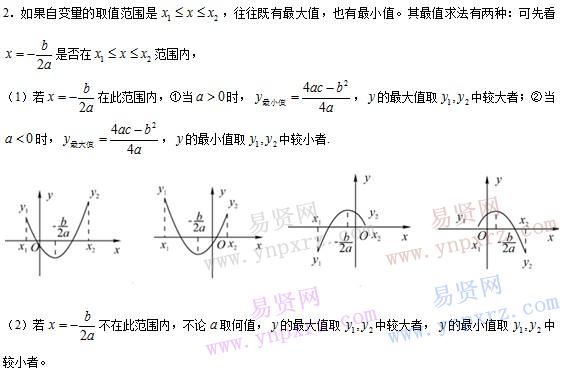
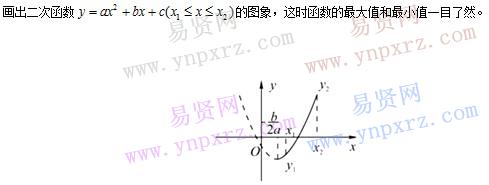
1.如果自变量的取值是全体实数,那么二次函数在图象顶点处取到最大值(或最小值)。
这时有两种方法求最值:一种是利用顶点坐标公式,一种是利用配方计算。

二.二次函数与一元二次方程、二次三项式的关系
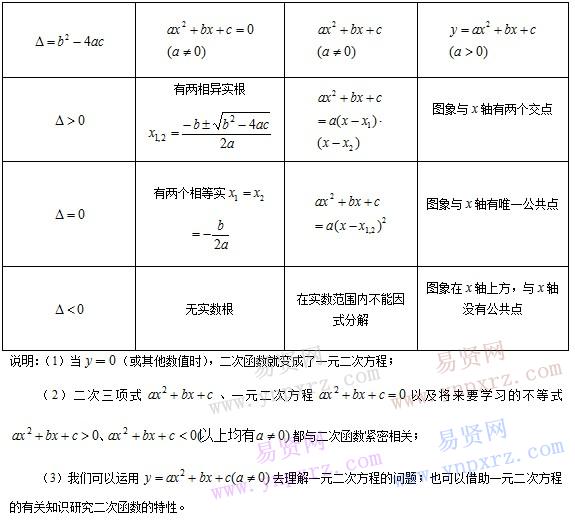
三.二次函数的实际应用
在公路、桥梁、隧道、城市建设等很多方面都有抛物线型;生产和生活中,有很多“利润最大”、“用料最少”、“开支最节约”、“线路最短”、“面积最大”等问题,它们都有可能用到二次函数关系,用到二次函数的最值。
那么解决这类问题的一般步骤是:
第一步:设自变量;
第二步:建立函数解析式;
第三步:确定自变量取值范围;
第四步:根据顶点坐标公式或配方法求出最值(在自变量的取值范围内)。
常见考法
(1)考查一些带约束条件的二次函数最值;
(2)结合二次函数考查一些创新问题。
误区提醒
(1)忽略自变量的取值范围,所求最值不符合实际意义;
(2)二次函数的坐标系建立的不恰当,给解题带来了困难。
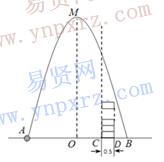
【典型例题】(2010 四川南充)如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?

推荐信息